Xi4or0uji's blog

RSA初探

RSA
字数统计: 3.4k阅读时长: 18 min
2019/02/12 Share

最近要给新生们出密码学的题，密码学白痴小肉鸡枯了，只能先学一波

简单概要

rsa是非对称加密，具体非对称加密是什么就不解释了，网上也有很多介绍，接下来我们直接进入加解密的过程
1、选择两个较大的互不相等的质数p和q，计算 n = p * q
2、计算 φ = (p-1) * (q-1)
3、选取任意e，使得1 < e < φ，而且 gcd ( e , φ ) = 1
4、计算e关于φ的模逆元d，即 ( e * d ) % φ = 1
5、加解密：c = ( m ^ e ) % n，m = ( c ^ d ) % n，c为密文，m为明文，(n,e)为公钥对，(n,d)为私钥对

模逆运算

如果( a * b ) % c = 1，那么a和b互为对方模c的模逆元或叫数论倒数，也写成

假设a和b两个数互为质数，即gcd ( a , b ) = 1时，有 ax + by = 1，所以 ( a * x ) % b = 1，x就是a对b的模逆元，因此，a对b存在模逆元x的充要条件是 gcd ( a , b ) = 1，对于每一组ab，存在一组满足条件的x，在求逆元的时候取最小正整数解 x mod n
简单证明

1
2
3
4
5
6
7
8
9
证：给予两个整数a、b，必然存在整数x、y使得ax+by=gcd(a,b)
两边除gcd(a,b)，右边成了1，左边a和b除了gcd(a,b)以后，新的a和b就互质
即证明ax+by=1 gcd(a,b)=1有整数解
想要证明ax+by=1 ab互质有整数解，那就是证明(a%b)*x1+b*y1=1有解
又辗转相除法可知，gcd(a,b)=gcd(b,a%b)，即ab互质则b和a%b也会互质
让a=b,b=a%b，可得b*x1+(a%b)*y1=1
继续a=a%b,b=((a%b)%b)，可得(a%b)*x2+((a%b)%b)*y2=1
...
最后得到a=1,b=0，即1*xn+0*yn=1，显然成立，证毕

求逆元方法
欧几里得算法

1
2
3
4
5
6
7
8
9
def egcd(a,b):
    if b==0:
        return 1,0,a
    else:
        x,y,q = egcd(b,a%b) #gcd(a,b) = gcd(b,a%b)
        x,y = y,(x-(a//b)*y)
        return x,y,q
def mod_inv(a,b):
    return egcd(a,b)[0]%b #求a模b得逆元

gmpy2库

1
2
import gmpy2
print gmpy2.invert(47,30)

欧几里得算法

就是辗转相除法

1
2
def gcd(a,b):
    return a if not b else gcd(b,a%b)

扩展欧几里得算法

就是上面求逆元的那个迭代

1
2
3
4
5
6
7
def egcd(a,b):
    if(b==0):
        return 1,0,a
    else:
        x1,y1,q = egcd(b,a%b)
        x,y = y1,(x1-(a//b)*y1)
        return x,y,q

例题

概念题

jarvisoj veryeasyRSA

题目给了pqe三个值，要求算d

1
2
3
p = 3487583947589437589237958723892346254777 
q = 8767867843568934765983476584376578389
e = 65537

当然可以手工算，也可以直接扔去rsatool去算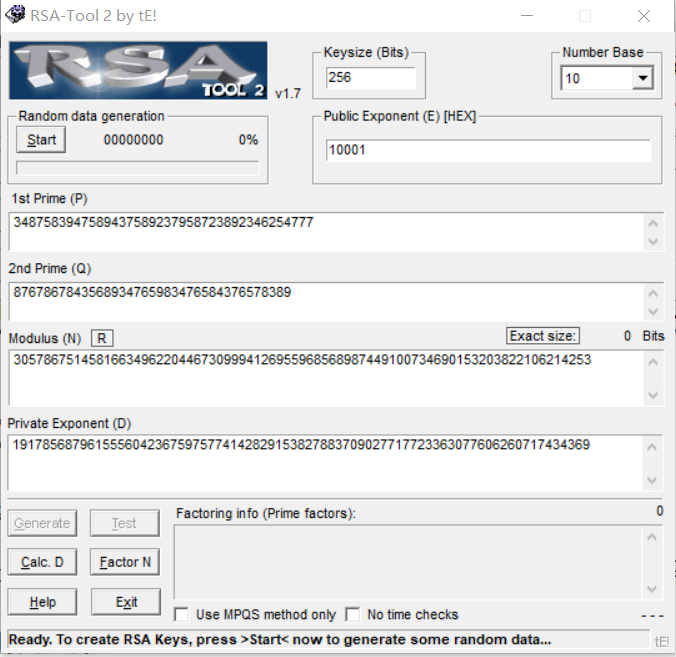

jarvisoj Easy RSA

这题比起原来的题稍微难一点点，给了n，e和密文，要求算明文

1
2
已知一段RSA加密的信息为：0xdc2eeeb2782c且已知加密所用的公钥：
(N=322831561921859 e = 23)

先去factordb.com分解一下n，算出p和q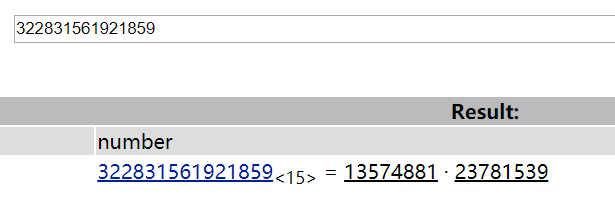

算出p=13574881，q=23781539，然后rsatool算d，最后直接大数运算乘出来
m = ( c ^ d ) % n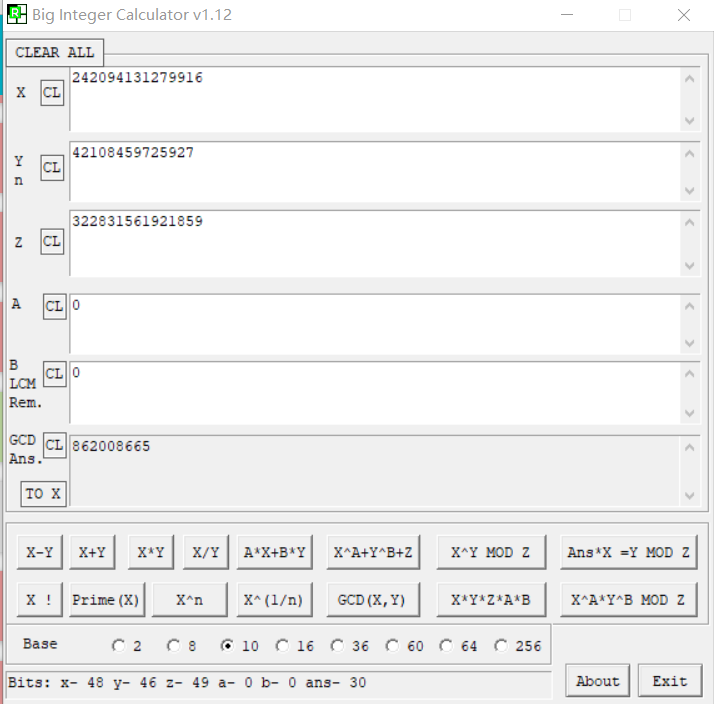

最后将它转成字符串就行

模数相关攻击

直接分解n

攻击条件

当n小于512位时，可以直接大数分解得到p和q

jarvisoj medium rsa

题目给了flag.enc和pubkey.pem文件，先用openssl命令提取信息

1
openssl rsa -pubin -in pubkey.pem -text -modulus

得到

1
2
3
4
5
6
7
8
9
10
11
12
Public-Key: (256 bit)
Modulus:
    00:c2:63:6a:e5:c3:d8:e4:3f:fb:97:ab:09:02:8f:
    1a:ac:6c:0b:f6:cd:3d:70:eb:ca:28:1b:ff:e9:7f:
    be:30:dd
Exponent: 65537 (0x10001)
Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD
writing RSA key
-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE=
-----END PUBLIC KEY-----

可以知道n是0xC2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD
数字不大，直接放去factordb.com分解一下得到

1
2
p=275127860351348928173285174381581152299
q=319576316814478949870590164193048041239

然后解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import libnum
from Crypto.Util.number import long_to_bytes

p=275127860351348928173285174381581152299
q=319576316814478949870590164193048041239
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
e = 65537

d = libnum.invmod(e,(p-1)*(q-1))
with open('flag.enc','r') as f:
    c = f.read().encode('hex')
    c = int(c,16)
m = pow(c,d,n)
print long_to_bytes(m)

p和q选取不当使n可分解

攻击条件

如果p和q选择不当，使得n可以快速分解
|p-q|较大
如果p-q很大，那么会有一个数很小，因此可以直接穷举法求出p和q，但是这只是理想
|p-q|较小
先看一条等式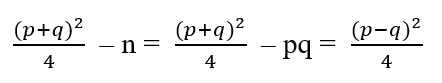

因为|p-q|较小，所以(p-q)²/4也会比较小，因此(p+q)²/4和n相差不大，所以(p+q)/2与√n相近，因此可以这样分解：
遍历从1开始一直到√n的整数，直到找到一个整数x满足x² - n是平方数，记做y²，就有x² - n = y²，然后就能根据平方差公式分解出n
p-1光滑
当p是n的因数，而且p-1是光滑的，可以使用Pollard’s p-1算法分解n
p+1光滑
当p时n的因数，而且p+1是光滑的，可以使用William’s p+1算法分解n

SECCON2017 very smooth

拿到一个pcap文件，分离一下

1
binwalk -e s.pcap

然后就会有三个证书文件，15A5.crt 8F4.crt FC6.crt
提一下信息

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
openssl x509 -inform der -in FC6.crt -pubkey -text -modulus -noout
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDVRqqCXPYd6Xdl9GT7/kiJrYvy
8lohddAsi28qwMXCe2cDWuwZKzdB3R9NEnUxsHqwEuuGJBwJwIFJnmnvWurHjcYj
DUddp+4X8C9jtvCaLTgd+baSjo2eB0f+uiSL/9/4nN+vR3FliRm2mByeFCjppTQl
yioxCqbXYIMxGO4NcQIDAQAB
-----END PUBLIC KEY-----
Certificate:
    Data:
        Version: 1 (0x0)
        Serial Number:
            a1:8b:63:0c:7b:30:99:df
    Signature Algorithm: sha256WithRSAEncryption
        Issuer: C = JP, ST = Kawasaki, O = SRL
        Validity
            Not Before: Oct  8 02:47:17 2017 GMT
            Not After : Oct  8 02:47:17 2018 GMT
        Subject: C = JP, ST = Kawasaki, O = SRL
        Subject Public Key Info:
            Public Key Algorithm: rsaEncryption
                Public-Key: (1024 bit)
                Modulus:
                    00:d5:46:aa:82:5c:f6:1d:e9:77:65:f4:64:fb:fe:
                    48:89:ad:8b:f2:f2:5a:21:75:d0:2c:8b:6f:2a:c0:
                    c5:c2:7b:67:03:5a:ec:19:2b:37:41:dd:1f:4d:12:
                    75:31:b0:7a:b0:12:eb:86:24:1c:09:c0:81:49:9e:
                    69:ef:5a:ea:c7:8d:c6:23:0d:47:5d:a7:ee:17:f0:
                    2f:63:b6:f0:9a:2d:38:1d:f9:b6:92:8e:8d:9e:07:
                    47:fe:ba:24:8b:ff:df:f8:9c:df:af:47:71:65:89:
                    19:b6:98:1c:9e:14:28:e9:a5:34:25:ca:2a:31:0a:
                    a6:d7:60:83:31:18:ee:0d:71
                Exponent: 65537 (0x10001)
    Signature Algorithm: sha256WithRSAEncryption
         78:92:11:fb:6c:e1:7a:f7:2a:33:b8:8b:08:a7:f7:5b:de:cf:
         62:0b:a0:ed:be:d0:69:88:38:93:94:9d:05:41:73:bd:7e:b3:
         32:ec:8e:10:bc:3a:62:b0:56:c7:c1:3f:60:66:a7:be:b9:46:
         f7:46:22:6a:f3:5a:25:d5:66:94:57:0e:fc:b5:16:33:05:1c:
         6f:f5:85:74:57:a4:a0:c6:ce:4f:fd:64:53:94:a9:83:b8:96:
         bf:5b:a7:ee:8b:1e:48:a7:d2:43:06:0e:4f:5a:86:62:69:05:
         e2:c0:bd:4e:89:c9:af:04:4a:77:a2:34:86:6a:b8:d2:3b:32:
         b7:39
Modulus=D546AA825CF61DE97765F464FBFE4889AD8BF2F25A2175D02C8B6F2AC0C5C27B67035AEC192B3741DD1F4D127531B07AB012EB86241C09C081499E69EF5AEAC78DC6230D475DA7EE17F02F63B6F09A2D381DF9B6928E8D9E0747FEBA248BFFDFF89CDFAF4771658919B6981C9E1428E9A53425CA2A310AA6D760833118EE0D71

openssl x509 -inform der -in 15A5.crt -pubkey -text -modulus -noout
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDVRqqCXPYd6Xdl9GT7/kiJrYvy
8lohddAsi28qwMXCe2cDWuwZKzdB3R9NEnUxsHqwEuuGJBwJwIFJnmnvWurHjcYj
DUddp+4X8C9jtvCaLTgd+baSjo2eB0f+uiSL/9/4nN+vR3FliRm2mByeFCjppTQl
yioxCqbXYIMxGO4NcQIDAQAB
-----END PUBLIC KEY-----
Certificate:
    Data:
        Version: 1 (0x0)
        Serial Number:
            a1:8b:63:0c:7b:30:99:df
    Signature Algorithm: sha256WithRSAEncryption
        Issuer: C = JP, ST = Kawasaki, O = SRL
        Validity
            Not Before: Oct  8 02:47:17 2017 GMT
            Not After : Oct  8 02:47:17 2018 GMT
        Subject: C = JP, ST = Kawasaki, O = SRL
        Subject Public Key Info:
            Public Key Algorithm: rsaEncryption
                Public-Key: (1024 bit)
                Modulus:
                    00:d5:46:aa:82:5c:f6:1d:e9:77:65:f4:64:fb:fe:
                    48:89:ad:8b:f2:f2:5a:21:75:d0:2c:8b:6f:2a:c0:
                    c5:c2:7b:67:03:5a:ec:19:2b:37:41:dd:1f:4d:12:
                    75:31:b0:7a:b0:12:eb:86:24:1c:09:c0:81:49:9e:
                    69:ef:5a:ea:c7:8d:c6:23:0d:47:5d:a7:ee:17:f0:
                    2f:63:b6:f0:9a:2d:38:1d:f9:b6:92:8e:8d:9e:07:
                    47:fe:ba:24:8b:ff:df:f8:9c:df:af:47:71:65:89:
                    19:b6:98:1c:9e:14:28:e9:a5:34:25:ca:2a:31:0a:
                    a6:d7:60:83:31:18:ee:0d:71
                Exponent: 65537 (0x10001)
    Signature Algorithm: sha256WithRSAEncryption
         78:92:11:fb:6c:e1:7a:f7:2a:33:b8:8b:08:a7:f7:5b:de:cf:
         62:0b:a0:ed:be:d0:69:88:38:93:94:9d:05:41:73:bd:7e:b3:
         32:ec:8e:10:bc:3a:62:b0:56:c7:c1:3f:60:66:a7:be:b9:46:
         f7:46:22:6a:f3:5a:25:d5:66:94:57:0e:fc:b5:16:33:05:1c:
         6f:f5:85:74:57:a4:a0:c6:ce:4f:fd:64:53:94:a9:83:b8:96:
         bf:5b:a7:ee:8b:1e:48:a7:d2:43:06:0e:4f:5a:86:62:69:05:
         e2:c0:bd:4e:89:c9:af:04:4a:77:a2:34:86:6a:b8:d2:3b:32:
         b7:39
Modulus=D546AA825CF61DE97765F464FBFE4889AD8BF2F25A2175D02C8B6F2AC0C5C27B67035AEC192B3741DD1F4D127531B07AB012EB86241C09C081499E69EF5AEAC78DC6230D475DA7EE17F02F63B6F09A2D381DF9B6928E8D9E0747FEBA248BFFDFF89CDFAF4771658919B6981C9E1428E9A53425CA2A310AA6D760833118EE0D71

openssl x509 -inform der -in 8F4.crt -pubkey -text -modulus -noout
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDVRqqCXPYd6Xdl9GT7/kiJrYvy
8lohddAsi28qwMXCe2cDWuwZKzdB3R9NEnUxsHqwEuuGJBwJwIFJnmnvWurHjcYj
DUddp+4X8C9jtvCaLTgd+baSjo2eB0f+uiSL/9/4nN+vR3FliRm2mByeFCjppTQl
yioxCqbXYIMxGO4NcQIDAQAB
-----END PUBLIC KEY-----
Certificate:
    Data:
        Version: 1 (0x0)
        Serial Number:
            a1:8b:63:0c:7b:30:99:df
    Signature Algorithm: sha256WithRSAEncryption
        Issuer: C = JP, ST = Kawasaki, O = SRL
        Validity
            Not Before: Oct  8 02:47:17 2017 GMT
            Not After : Oct  8 02:47:17 2018 GMT
        Subject: C = JP, ST = Kawasaki, O = SRL
        Subject Public Key Info:
            Public Key Algorithm: rsaEncryption
                Public-Key: (1024 bit)
                Modulus:
                    00:d5:46:aa:82:5c:f6:1d:e9:77:65:f4:64:fb:fe:
                    48:89:ad:8b:f2:f2:5a:21:75:d0:2c:8b:6f:2a:c0:
                    c5:c2:7b:67:03:5a:ec:19:2b:37:41:dd:1f:4d:12:
                    75:31:b0:7a:b0:12:eb:86:24:1c:09:c0:81:49:9e:
                    69:ef:5a:ea:c7:8d:c6:23:0d:47:5d:a7:ee:17:f0:
                    2f:63:b6:f0:9a:2d:38:1d:f9:b6:92:8e:8d:9e:07:
                    47:fe:ba:24:8b:ff:df:f8:9c:df:af:47:71:65:89:
                    19:b6:98:1c:9e:14:28:e9:a5:34:25:ca:2a:31:0a:
                    a6:d7:60:83:31:18:ee:0d:71
                Exponent: 65537 (0x10001)
    Signature Algorithm: sha256WithRSAEncryption
         78:92:11:fb:6c:e1:7a:f7:2a:33:b8:8b:08:a7:f7:5b:de:cf:
         62:0b:a0:ed:be:d0:69:88:38:93:94:9d:05:41:73:bd:7e:b3:
         32:ec:8e:10:bc:3a:62:b0:56:c7:c1:3f:60:66:a7:be:b9:46:
         f7:46:22:6a:f3:5a:25:d5:66:94:57:0e:fc:b5:16:33:05:1c:
         6f:f5:85:74:57:a4:a0:c6:ce:4f:fd:64:53:94:a9:83:b8:96:
         bf:5b:a7:ee:8b:1e:48:a7:d2:43:06:0e:4f:5a:86:62:69:05:
         e2:c0:bd:4e:89:c9:af:04:4a:77:a2:34:86:6a:b8:d2:3b:32:
         b7:39
Modulus=D546AA825CF61DE97765F464FBFE4889AD8BF2F25A2175D02C8B6F2AC0C5C27B67035AEC192B3741DD1F4D127531B07AB012EB86241C09C081499E69EF5AEAC78DC6230D475DA7EE17F02F63B6F09A2D381DF9B6928E8D9E0747FEBA248BFFDFF89CDFAF4771658919B6981C9E1428E9A53425CA2A310AA6D760833118EE0D71

待续……

模不互素

攻击条件

存在两个或以上模数，且gcd(n1,n2)!=1

攻击原理

如果两个n不互素的话，可以直接对这两个数求最大公因数，然后获得p和q，进而求得私钥

SCTF RSA2

公钥指数相关攻击

小公钥指数攻击

攻击条件

e十分小

例子

假设用户使用的密钥为3，加密过程是

1
c ≡ m³ mod n

那么就有

1
2
m³ = c + k*n
m = ³√¯(c+k*n)¯

大黑阔可以从小到大枚举k，直到开出整数

jarvisoj Extremely hard RSA

题目给了pubkey.pem和flag.enc，然后openssl读下pubkey信息有

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
Public-Key: (4096 bit)
Modulus:
    00:b0:be:e5:e3:e9:e5:a7:e8:d0:0b:49:33:55:c6:
    18:fc:8c:7d:7d:03:b8:2e:40:99:51:c1:82:f3:98:
    de:e3:10:45:80:e7:ba:70:d3:83:ae:53:11:47:56:
    56:e8:a9:64:d3:80:cb:15:7f:48:c9:51:ad:fa:65:
    db:0b:12:2c:a4:0e:42:fa:70:91:89:b7:19:a4:f0:
    d7:46:e2:f6:06:9b:af:11:ce:bd:65:0f:14:b9:3c:
    97:73:52:fd:13:b1:ee:a6:d6:e1:da:77:55:02:ab:
    ff:89:d3:a8:b3:61:5f:d0:db:49:b8:8a:97:6b:c2:
    05:68:48:92:84:e1:81:f6:f1:1e:27:08:91:c8:ef:
    80:01:7b:ad:23:8e:36:30:39:a4:58:47:0f:17:49:
    10:1b:c2:99:49:d3:a4:f4:03:8d:46:39:38:85:15:
    79:c7:52:5a:69:98:4f:15:b5:66:7f:34:20:9b:70:
    eb:26:11:36:94:7f:a1:23:e5:49:df:ff:00:60:18:
    83:af:d9:36:fe:41:1e:00:6e:4e:93:d1:a0:0b:0f:
    ea:54:1b:bf:c8:c5:18:6c:b6:22:05:03:a9:4b:24:
    13:11:0d:64:0c:77:ea:54:ba:32:20:fc:8f:4c:c6:
    ce:77:15:1e:29:b3:e0:65:78:c4:78:bd:1b:eb:e0:
    45:89:ef:9a:19:7f:6f:80:6d:b8:b3:ec:d8:26:ca:
    d2:4f:53:24:cc:de:c6:e8:fe:ad:2c:21:50:06:86:
    02:c8:dc:dc:59:40:2c:ca:c9:42:4b:79:00:48:cc:
    dd:93:27:06:80:95:ef:a0:10:b7:f1:96:c7:4b:a8:
    c3:7b:12:8f:9e:14:11:75:16:33:f7:8b:7b:9e:56:
    f7:1f:77:a1:b4:da:ad:3f:c5:4b:5e:7e:f9:35:d9:
    a7:2f:b1:76:75:97:65:52:2b:4b:bc:02:e3:14:d5:
    c0:6b:64:d5:05:4b:7b:09:6c:60:12:36:e6:cc:f4:
    5b:5e:61:1c:80:5d:33:5d:ba:b0:c3:5d:22:6c:c2:
    08:d8:ce:47:36:ba:39:a0:35:44:26:fa:e0:06:c7:
    fe:52:d5:26:7d:cf:b9:c3:88:4f:51:fd:df:df:4a:
    97:94:bc:fe:0e:15:57:11:37:49:e6:c8:ef:42:1d:
    ba:26:3a:ff:68:73:9c:e0:0e:d8:0f:d0:02:2e:f9:
    2d:34:88:f7:6d:eb:62:bd:ef:7b:ea:60:26:f2:2a:
    1d:25:aa:2a:92:d1:24:41:4a:80:21:fe:0c:17:4b:
    98:03:e6:bb:5f:ad:75:e1:86:a9:46:a1:72:80:77:
    0f:12:43:f4:38:74:46:cc:ce:b2:22:2a:96:5c:c3:
    0b:39:29
Exponent: 3 (0x3)
Modulus=B0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929
writing RSA key
-----BEGIN PUBLIC KEY-----
MIICIDANBgkqhkiG9w0BAQEFAAOCAg0AMIICCAKCAgEAsL7l4+nlp+jQC0kzVcYY
/Ix9fQO4LkCZUcGC85je4xBFgOe6cNODrlMRR1ZW6Klk04DLFX9IyVGt+mXbCxIs
pA5C+nCRibcZpPDXRuL2BpuvEc69ZQ8UuTyXc1L9E7Huptbh2ndVAqv/idOos2Ff
0NtJuIqXa8IFaEiShOGB9vEeJwiRyO+AAXutI442MDmkWEcPF0kQG8KZSdOk9AON
Rjk4hRV5x1JaaZhPFbVmfzQgm3DrJhE2lH+hI+VJ3/8AYBiDr9k2/kEeAG5Ok9Gg
Cw/qVBu/yMUYbLYiBQOpSyQTEQ1kDHfqVLoyIPyPTMbOdxUeKbPgZXjEeL0b6+BF
ie+aGX9vgG24s+zYJsrST1MkzN7G6P6tLCFQBoYCyNzcWUAsyslCS3kASMzdkycG
gJXvoBC38ZbHS6jDexKPnhQRdRYz94t7nlb3H3ehtNqtP8VLXn75NdmnL7F2dZdl
UitLvALjFNXAa2TVBUt7CWxgEjbmzPRbXmEcgF0zXbqww10ibMII2M5HNro5oDVE
JvrgBsf+UtUmfc+5w4hPUf3f30qXlLz+DhVXETdJ5sjvQh26Jjr/aHOc4A7YD9AC
LvktNIj3betive976mAm8iodJaoqktEkQUqAIf4MF0uYA+a7X6114YapRqFygHcP
EkP0OHRGzM6yIiqWXMMLOSkCAQM=
-----END PUBLIC KEY-----

e很小，所以我们可以直接进行指数攻击

1
2
3
4
5
6
7
8
9
10
11
12
13
import gmpy2,libnum
n=0xB0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929
e=3
res=0
c=int(open('flag.enc','rb').read().encode('hex'),16)
for k in range(118700000, 118750000):
    a, b = gmpy2.iroot(c+n*k,e)
    if b==1:
        res=a
        print k
        print res
        print libnum.n2s(res)
        break

他的k是118719488，减小范围，跑的快一点，最后拿到flag

1
Didn't you know RSA padding is really important? Now you see a non-padding message is so dangerous. And you should notice this in future.Fl4g: PCTF{Sm4ll_3xpon3nt_i5_W3ak}

rabin算法

攻击条件

e = 2

攻击原理

密文

1
c = m² mod n

解密过程

1
2
3
4
5
6
7
8
9
10
算mp和mq
mp = √c mod p
mq = √c mod q
由扩展欧几里得算出
yp*p + yq*q = 1
得到四个明文
a = (yp*p*mq + yq*q*mp) mod n
b = n - a
c = (yp*p*mq - yq*q*mp) mod n
d = n - c

如果 p ≡ q ≡ 3 (mod 4)，那么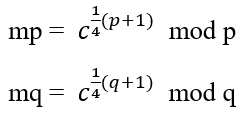

jarvisoj hardRSA

openssl提信息

1
2
3
4
5
6
7
8
9
10
11
12
Public-Key: (256 bit)
Modulus:
    00:c2:63:6a:e5:c3:d8:e4:3f:fb:97:ab:09:02:8f:
    1a:ac:6c:0b:f6:cd:3d:70:eb:ca:28:1b:ff:e9:7f:
    be:30:dd
Exponent: 2 (0x2)
Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD
writing RSA key
-----BEGIN PUBLIC KEY-----
MDowDQYJKoZIhvcNAQEBBQADKQAwJgIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgEC
-----END PUBLIC KEY-----

分解n得到

1
2
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239

利用rabin算法去写脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#!/usr/bin/python
# coding:utf-8
import gmpy2
import string
from Crypto.PublicKey import RSA

with open('pubkey.pem','r') as f:
    key = RSA.importKey(f)
    n = key.n
    e = key.e

with open('flag.enc','r') as f:
    c = f.read().encode('hex')
    c = string.atoi(c,base=16)

print "start"
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
#计算yp和yq
inv_p = gmpy2.invert(p,q)
inv_q = gmpy2.invert(q,p)
#计算mp和mq
mp = pow(c,(p+1)/4,p)
mq = pow(c,(q+1)/4,q)
#算a b c d
a = (inv_p * p * mq + inv_q * q * mp) % n
b = n - int(n)
c = (inv_p * p * mq - inv_q * q * mp) % n
d = n - int(c)

for i in (a,b,c,d):
    s = '%x' % i
    if len(s) % 2 != 0:
        s = '0'+s
    print s.decode('hex')

最后拿到flag：PCTF{sp3ci4l_rsa}

CATALOG
  1. 1. 简单概要
    1. 1.1. 模逆运算
  2. 2. 欧几里得算法
  3. 3. 扩展欧几里得算法
  4. 4. 例题
    1. 4.1. 概念题
      1. 4.1.1. jarvisoj veryeasyRSA
      2. 4.1.2. jarvisoj Easy RSA
    2. 4.2. 模数相关攻击
      1. 4.2.1. 直接分解n
        1. 4.2.1.1. 攻击条件
        2. 4.2.1.2. jarvisoj medium rsa
      2. 4.2.2. p和q选取不当使n可分解
        1. 4.2.2.1. 攻击条件
        2. 4.2.2.2. SECCON2017 very smooth
      3. 4.2.3. 模不互素
        1. 4.2.3.1. 攻击条件
        2. 4.2.3.2. 攻击原理
        3. 4.2.3.3. SCTF RSA2
    3. 4.3. 公钥指数相关攻击
      1. 4.3.1. 小公钥指数攻击
        1. 4.3.1.1. 攻击条件
        2. 4.3.1.2. 例子
        3. 4.3.1.3. jarvisoj Extremely hard RSA
      2. 4.3.2. rabin算法
        1. 4.3.2.1. 攻击条件
        2. 4.3.2.2. 攻击原理
        3. 4.3.2.3. jarvisoj hardRSA
Total : 68
2020
2019
2018
CTF 安恒杯 MongoDB Code Breaking java php_tricks cve javascript python xss web+re SQL 端口转发 upload docker Code_Breaking HTTP laravel mysql xxe LFSR RSA serialize php-fpm
CTF WEB CVE docker CRYPTO